Patterns exist everywhere!  From quilts to tile floors to patterns that exist in nature, our brains are wired to find patterns.

Looking for a pattern is a very useful strategy when solving math problems.  In many cases, this strategy is combined with other strategies to find the solution to the problem.

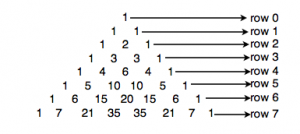
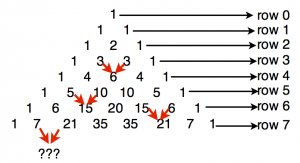
To introduce students to finding patterns and sequences, we looked at Fibonacci’s Sequence and Pascal’s Triangle .  This is what Pascal’s Triangle looks like.  Do you see any patterns?  Can you tell what numbers will be in row 7?

Don’t Peak!  See if you can figure out the pattern!

What numbers will be in the 8th row?  What will the first two numbers be in the 100th row?  Can you use a pattern to answer these questions?  What other questions can you come up with about Pascal’s Triangle?  What other interesting information can you find out about Pascal’s Triangle?

Here is Fibonacci’s Sequence.  Do you see the pattern?  What will the next three terms be?

Think you’ve got it?  Don’t peak!

If you came up with 34, 55, and 89, then you are correct!  What other questions can you ask about Fibonacci’s Sequence?  Where does Fibonacci’s Sequence show up in nature?  What other information can you find out about Fibonacci?